前言
对很多研究国学传统文化,和《易》学的人中,大部分都是把取象比类的方向,带向哲学和文科方向,其实从数学逻辑也是可以寻找到其中的踪迹的。
人类历史的进程,科学的发展,优秀的思维方式是互相借鉴的。
取象比类
关于取象比类,很多人会立马联想到伏羲造八卦的过程。
“古者包牺氏之王天下也,仰则观象于天,俯则观法于地,观鸟兽之文,与地之宜,近取诸身,远取诸物,于是始作八卦。”
这一段记载,通常简述为“伏羲观天法地,而作八卦”,是对古代观象授时的最为古老的记载,同时也说到八卦的起源,以及《易经》与观象授时的关系。对这一段记载的正确诠释,将有助于我们深入理解和研究《周易》。
伏羲上观天象,下法于地。
取象的方法可以有很多种,比如:位置、特性、时间、空间、大小、颜色、状态、声音、外观、数字、符号等等,看起来没有固定的公式,会随着时代或者环境而变化,但是万象不离其宗。
八卦:乾兑离震巽坎艮坤,就是对这些象的高度浓缩和提取。
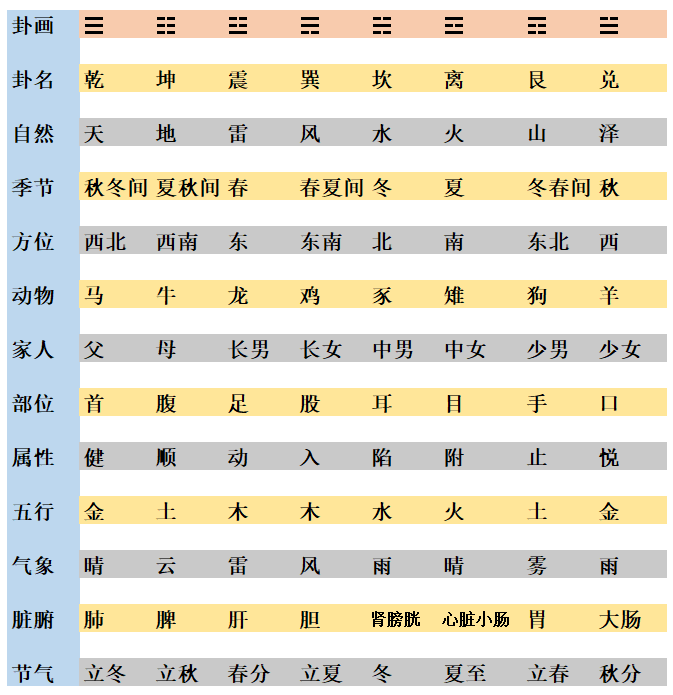
常用的八卦属性配置表,如下:
上图A:八卦配属表
取象比类是中国古代一种天人合一的世界观和思维方式。
当八卦的数象理模式给发明出来的,这已然是一个独特的数学体系,只不过现在世界的科学主流并没有直接承认其系统性和优越性,其实也是外国人看不懂,当然很多中国人自己也搞不懂。
花开两支,按下不表,我们来看看数学历史上,对数的产生的情形,寻找一些启发。
对数的产生
十五世纪伟大天才数学家纳皮尔,也是一位天文学家,为了技术复杂而庞大的行星轨道数据,发明了对数运算。
“看起来在数学实践中,最麻烦的莫过于大数字的乘法、除法、开平方和开立方,计算起来特别费事又伤脑筋,于是我开始构思有什么巧妙好用的方法可以解决这些问题。”
长期枯燥而重复的计算差别不大的天文数字,天才都会想办法走捷径,用更简洁的办法,快速的计算出这些庞大数字的运算结果。
纳皮尔不是一般人,不想像IT民工一样苦逼的重复搬砖,于是用了20年的时间,进行了数百万次的计算,发明了对数和对数表,其实就是一个脚本了。
在数学中,对数是对求幂的逆运算,正如除法是乘法的逆运算,反之亦然。
这意味着一个数字的对数是必须产生另一个固定数字(基数)的指数。 在简单的情况下,乘数中的对数计数因子。
更一般来说,乘幂允许将任何正实数提高到任何实际功率,总是产生正的结果,因此可以对于b不等于1的任何两个正实数b和x计算对数。
如果a的x次方等于N(a>0,且a≠1),那么数x叫做以a为底N的对数(logarithm),记作x=loga N。其中,a叫做对数的底数,N叫做真数。
求幂:a的x次方等于N(a>0,且a≠1)
对数:x=loga N。其中,a叫做对数的底数,N叫做真数
图一:对数
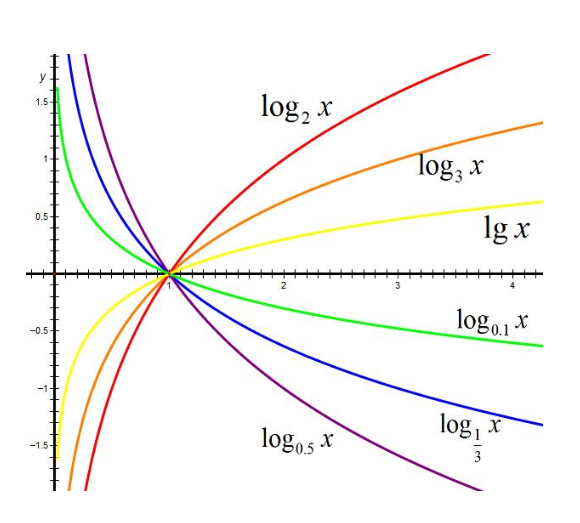
图二:幂函数
上述是关于对数和幂运算的描述,基本上都只是中学的内容。
为了简化模型,我们回到对数产生时候的应用场景。
等比数列和等差数列
我们列出一组等比数列和等差数列,如下表:
如果愿意,你可以把这个表拉得很长,列出更多复杂的对应关系,都是可以的。
根据上表,我们可以从等差数列做加法,来得到等比数列中相应的数的相乘的结果,比如:
等差数列:3+7=10,
则有,
等比数列:8*128=1024,
关系图,如下:
那么反过来,1024÷128=?
从10-7=3,查表得:8
是不是很简便,有没有一些启发了?
五花八门的计算器
事实上,十五世纪的数学家,研究呢各种对数尺子,甚至纳皮尔还发明了除法器和乘法器,在现在看来,这是难以想象的事情。
上图:对数卡尺。
上图:纳皮尔乘除器
纳皮尔在1617年发明了这款基于木棒的计算器,他以土耳其数学家Matrak·Nasuh所普及的格子乘法系统打造了它。这是一部令人惊叹的机器,能够做加减乘除运算,甚至能够求数的平方根。
然而这也不是唯一的孤本,很显然土耳其数学家Matrak·Nasuh的格子乘法系统也是一个很成熟的系统了。
这是科塔发明的计算器。如下图:
数字是通过设备侧边的滑片来输入,通过旋转设备顶部的摇杆来进行加减乘除。
科塔计算器的设计蓝图,则来自伟大的数学家莱布尼兹。
中国古代的计算器
那么,看了这么多奇工巧术,是不是又要开始自卑,中国人毫无建树了。
中国古老的计算器,就是它,如下图:
不错,就是算盘。
中国第一个人造卫星升空成功,就是靠算盘敲出来的。
成千数百的科技工作者,一起用算盘在计算卫星轨道数据的场面,脑补一下,肯定是非常 壮观的。
不要小看算盘这个东西,珠心算在当下的世界科研的江湖,还是有它独特的地位的。
说到珠心算,回归伏羲的“远取诸象,近取诸物”造八卦。
隐约可以感觉到中国老祖宗离超级计算机的发明应该很近很近。
说不定,哪一天人们会按照八卦原理来设计新型的计算机,也是有可能的。
邻人借物的超算过程
很多人看到这里,估计若有所思,但是还是不明白,取象比类和对数运算到底有什么联系,具体又是如何体现的。
我们就一起来看这个例子。
话说宋朝的超算科学家邵雍和他的儿子,在某年的冬天黄昏,酉时就是傍晚17点到19点的时候。
晚饭后两父子,围炉取暖,畅谈宇宙天地人生,家常长短。
这个时候,听到有人敲门,自述是邻居来借东西。
邵先生出声叫道,门口的邻居先别说借什么,之后就让他儿子练手起来,各自用中国古代的超算程式运算一番。
其过程大致如下:
邻居来敲门,第一次敲一次,很响声,之后又急促的连续的敲了五下。
于是就得出一个,乾上巽下的卦象。如下表:
按照《易经》乾上巽下天风姤卦,四爻动。
其中:乾一,巽五,酉十,得变爻:16÷6=2余4
感觉已经有纳皮尔对数运算器的味道了。
运算原理:
姤卦的第四阳爻变阴爻,得变卦为巽上巽下之巽卦,互卦中见见两个乾卦,本来卦中又一个乾卦,加起来有三个乾卦属金,两个巽卦属木,由此可见所借的东西为金属木器之物,又根据本卦乾一数巽五数,乾上巽下,乾卦金一般较短,巽卦木一般较长,基本可以判断是:金短木长之物。
邵雍的儿子判断是锄头。“金短木长的东西,又是劳动所用的器。所借的东西应是锄头。”
邵院士意味深长的说:“儿子啊,还是差点火候啊。金短木长之物,没错,当下急用于劳作也是没错。但是谁家夜里用锄头啊,我们大宋朝还没有发明电灯呢,想想冬天寒夜,急用劈柴烧火下炉取暖之器,一定是斧头。”
一问邻居所借何物?果真是要借斧头,姜还是老得辣。
无论多么厉害的超级计算机,还是要在实际的生产应用情景去运算,才能真正的服务人类,得到有价值的运算结果。
邵雍的《易经》推演模式,可以理解为多重“对数”运算的叠加,甚至融合了兼容性更强大的模糊运算因子。
抛砖引玉,欢迎大家指正!


















110X110.png)
110x110.png)






请登录之后再进行评论