二维数的奥秘系列四,Z10Mod解世界数学难题,《周髀算经》的价值
副标题:
二维数的奥秘系列四,用九维数和九九归一的原理来证明费马大定理,并且做出推广
二维数的奥秘系列四,用九维数九九归一来证明费马大定理,并推广
华夏中医人 谦和既济LoontaDC 2022-02-11
关于费马大定理,1993年6月24日,《纽约时报》以“终于听到了欢呼“找到了”,古老数学之谜获解”为大标题报道了一个头版头条消息。前一天,大西洋的另一边,一名40多岁的英国数学家宣布他已经解决了最著名的数学问题,一个看似简单却困扰了数学家350年的问题。处于兴奋之中的这位数学家庞是安德鲁.怀尔斯,他的母校是英国剑桥大学,现为美国新泽西洲的普林斯顿大学教授。在题为“模形式,椭圆曲线以及伽罗瓦表示”的三场系列讲演的最后,他激动地宣布了这一消息。怀尔斯博士用这句话结束讲演:“因此,这表明费马大定理是成立的。证毕。”
而费马当年却有一种非常巧妙的证明方法,因为书的扉页太小,写不下,这正是费马大定理的迷人之处,而且历来不少人尝试从初等数学来寻求突破和证明。
在十进制体系里面,所有的数的特征值一共有九个,我们继续沿用申子源的G数集说法,G数集={1,2,3,4,5,6,7,8,9}。
也就是Z10Mod(N)=n,N为自然数,n∈G数集={1,2,3,4,5,6,7,8,9}。
一维数:1,2,3,4,5,6,7,8,9
二维数:1,4,9,16,25,36,49,64,81
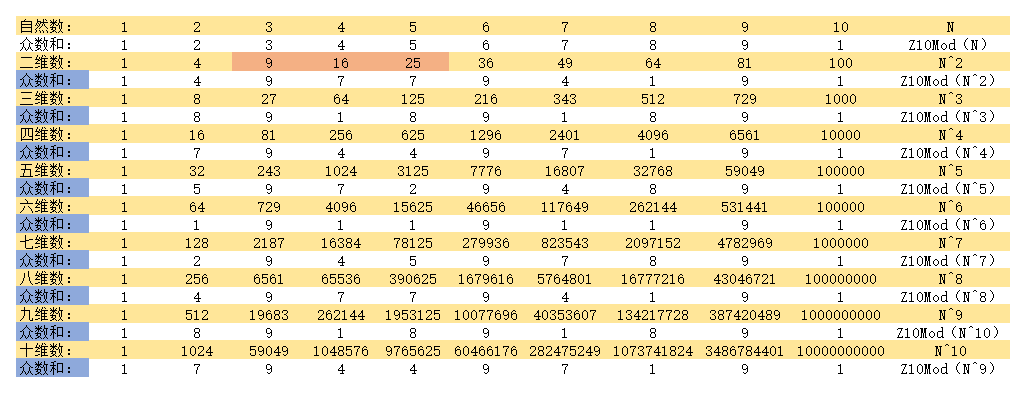
把一维数到十维数以及众数和(群数和),也就是其Z10Mod(N^n)值列表如下:
上图:表图一。
根据之前关于Z10Mod的定义和特性以及相关的结论。
根据Z10Mod(N)定义,我们可以对其作加法和乘法的运算。
Z10Mod(N)=n
Z10Mod(N)+Z10Mod(M)=Z10Mod(N+M)
Z10Mod(N)*Z10Mod(M)=Z10Mod(N*M)
Z10Mod(N^a)=Z10Mod(N^a)
其中:n∈(1,2,3,4,5,6,7,8,9),a∈自然数。
参考文章《二维数的奥秘系列二,众数和的mod定义,二十进制与十九数》。
简答来说,高于九维数,或者高于9数的n次方,都可以在上表找到相同的特征值。
这像几何的相似图形是原理,或者可以理解为一种映射和投影。
也可以理解为一种弱相关数特征。
在文章《从对数诞生的启发,打破取象比类的思维禁区,古代的超级计算机模型》中,
通过小数求大数,根据等比数列和等差数列的特征。
我们列出一组等比数列和等差数列,如下表:
如果愿意,你可以把这个表拉的很长,列出更多复杂的对应关系,都是可以的。
根据上表,我们可以从等差数列做加法,来得到等比数列中相应的数的相乘的结果,比如:
等差数列:3+7=10,
则有,
等比数列:8*128=1024,
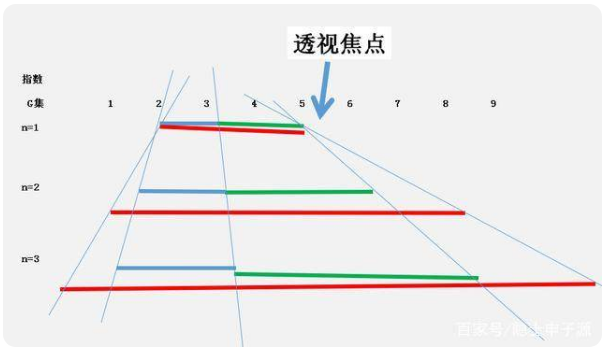
关系图,如下:
那么反过来,1024÷128=?
从10-7=3,查表得:8。
所以,要求X^n+Y^n=?Z^n,也就是费马大定理的内容。
只要验证表图一的结果就好。
在一维数域,也就是X^n+Y^n=?Z^n,当n=1的时候,有非常多的组合,这是小学的加法运算。
到了二维数域,也就是X^n+Y^n=?Z^n,当n=1的时候,只有一组数符合条件,也就是3^2+4^2=5^2,这也是有名的勾股定理。
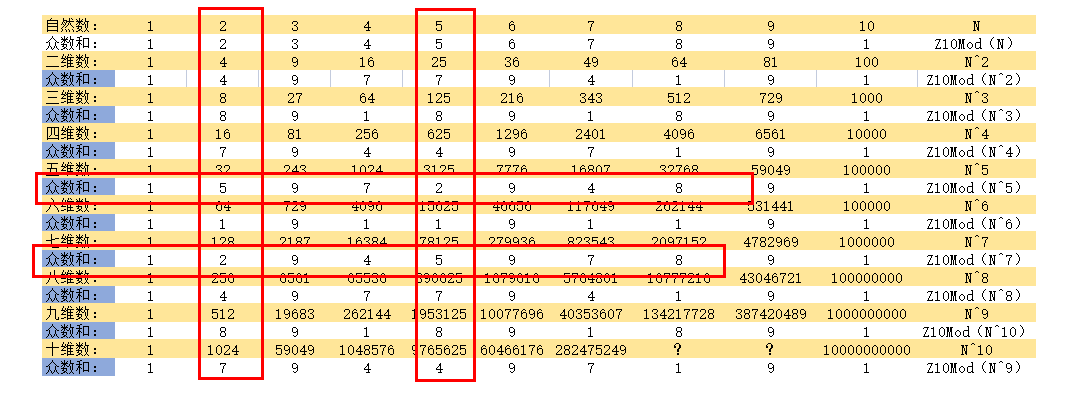
上图:图表二。
用Z10Mod运算3^2+4^2=?5^2的弱条件。
Z10Mod(3^2)=9,
Z10Mod(4^2)=7,
Z10Mod(5^2)=7,
Z10Mod(9+7)=7,
Z10Mod(3^2+4^2)=Z10Mod(3^2)+Z10Mod(4^2)=Z10Mod(5^2)成立,才继续验算:
3^2+4^2=5^2。
也就是对:X^n+Y^n=?Z^n,中:
如果:Z10Mod(X^n+Y^n)=Z10Mod(Y^n)+Z10Mod(Y^n)=Z10Mod(Z^n)不成立,则一定有:
X^n+Y^n≠Z^n,
事实上,对于n≥4的时候,在X,Y,Z∈G数集里面是不存在X^n+Y^n≠Z^n的。
证明如下:
对于X^n+Y^n=?Z^n,当n=4的时,
1,2,3,4,5,6,7,8,9,的4次方,
分别为:1,16,81,256,625,1296,2401,4096,6561,
其众数和Z10Mod值分别为:1,7,9,4,4,9,7,1,9,
根据特征,虽然有Z10Mod值数组:1,9,1,和9,4,4满足条件,同时检验N^n值的四次方间隔。
由于间隔数越来越大:
6561-4096>2401;
4096-2401>1296;
2401-1296>625;
1296-625>256;
625-256>81;
256-81>16;
81-16>1;
显然没有满足X^n+Y^n=Z^n的条件。每个数,减去和他差值最小的数,大于G集内的数的4次方的任一个数,意味着,不可能存在。
随着n值越来越大,也就是越高维度的数,显然是不存在:X^n+Y^n=Z^n的。
从数的维度出发,我们不妨猜想当n=3的时候,X^n+Y^n+Z^n=K^n,也就是:X^3+Y^3+Z^3=K^3,
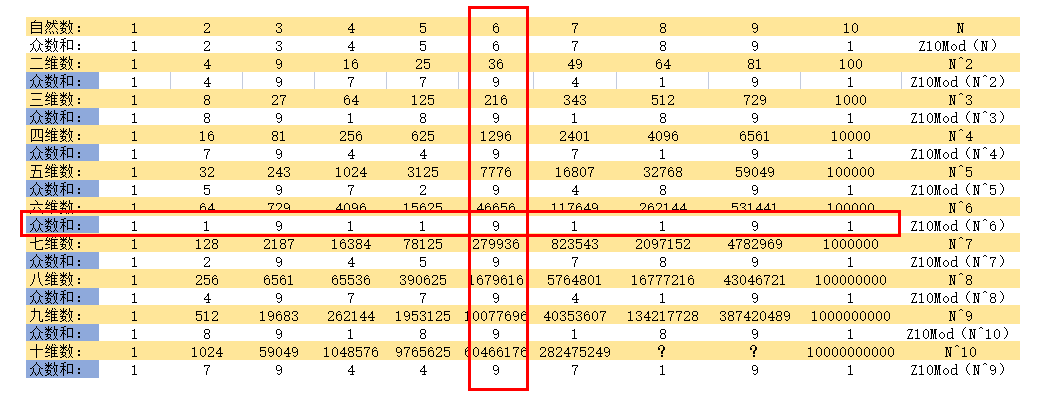
上图:表图三。
我们还找到这样一组数,1^3+6^3+8^3=9^3,
很显然灵活运用:
Z10Mod(1^3+6^3+8^3)
=Z10Mod[Z10Mod(1^3)+Z10Mod(6^3)+Z10Mod(8^3)]
=Z10Mod(1+9+8)
=9
=Z10Mod(9^3)
然后验算:1^3+6^3+8^3=9^3,可得。
这是费马大定理的一个推广和延伸。
《周髀算经》原文:”商高曰:数之法出于圆方,圆出于方,方出于矩,矩出于九九八十一。故折矩以为句广三、股修四、径隅五。既方其外,半之一矩,环而共盘,得成三四五。两矩共长二十有五,是谓积矩。故禹之所以治天下者,此数之所生也。”
中国古代数学认为,数的法则来源于园方,也就是规矩这个工具的运用。
圆形是由正方方形而来,正方形由矩形而来,而矩形是的源头在九数纵横的得来的。
大方无隅,正方形的极限会形成一个圆形。
正方形又是矩形(长方形)的极限情形。
九数纵横九可以组合任意的矩形。
九数纵横也是九九乘法表的基本原理。
也许古人赋予九九乘法表有更多深刻的数学内涵,我们想肤浅了,比如九维数和九数的组合运算。
现在的数学证明费马大定理是非常复杂的。
我们如果把勾股定理和费马大定理看成等价的,是一个非常有意思的问题,而和古代的河图数的九数系统有如此紧密的联系。
如果我们把这些维度的数看成是一种投影,那么在X^n+Y^n=Z^n,n=2,的约束下,有无限多的一维数相加的情形。
那么在X^n+Y^n+Z^n=K^n,n=3的约束下,X^2+Y^2+Z^2=K^2,也有无数解。
费马(1601-1665)是一名法国律师,他在业余时间从事数学研究,1637年他对看似很简单的方程x^n+y^n=z^n的可能整数解做了一个猜想。n=1时,这个方程是平凡的:任意两个整数和显然等于第三个整数。n=2的情况更有趣。有很多,实际上应该说有无穷多个整数三元组(x,y,z)满足x^2+y^2=z^2。这样的三元组很快让我们想到毕达哥拉斯定理。数学家要做的正是下一步,寻找x^3+y^3=z^3等的整数解。这事一直没有答案。
费马认为他证明了对任意大于2的n,这一方程没有正整数解。
如果从表图二看,n=3的整数解,必须要在X^n+Y^n+Z^n=K^n,n=3的表达式中去寻找,这九是数的维度,也是一个广义的九九乘法表的运用。
在求Z10ModN^n的值的时候出现一些奇妙的现象。
1、369数的所有Z10ModN^n值都是9,也就是:Z10Mod3^n=Z10Mod6^n=Z10Mod9^n=9,
这可以推测尼古拉.特斯拉把369数看成神秘的数,甚至看成宇宙的密码。
2,六维数和6数的特征非常奇特单纯。
3、二维数,四维数,八维数和十维数出现同构现象。
二进制,阴阳四象八卦在这里找到均衡的法则。
3,五维数和七维数出现的数字最多,两者基本同构。
2数和5数同构。
还有一些诸如此类的特征,就不一一列举了。
END
二维数的奥秘系列文章,完结。
参考文章:
《二维数的奥秘系列一,围棋盘纵横十九行,到底隐藏什么高深的数学原理》
《二维数的奥秘系列二,众数和的mod定义,二十进制与十九数》
《二维数的奥秘系列三,二维数是怎么一回事,有什么意义和价值》
《一种采用mod值构造G集合来证明费马大定理的方法》
《从对数诞生的启发,打破取象比类的思维禁区,古代的超级计算机模型》
END
















110X110.png)
110x110.png)






请登录之后再进行评论